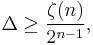Minkowski–Hlawka theorem

In mathematics, the Minkowski–Hlawka theorem is a result on the lattice packing of hyperspheres in dimension n > 1. It states that there is a lattice in Euclidean space of dimension n, such that the corresponding best packing of hyperspheres with centres at the lattice points has density Δ satisfying

$\Delta \geq \frac{\zeta(n)}{2^{n-1}},$

with ζ the Riemann zeta function. Here as n → ∞, ζ(n) → 1. The proof of this theorem is nonconstructive, however, and it is still not known how to construct lattices with packing densities exceeding this bound for arbitrary n.

This is a result of Hermann Minkowski (1905, not published) and Edmund Hlawka (1944). The result is related to a linear lower bound for the Hermite constant.

See aolso

Kepler conjecture

References

Conway, John H.; Neil J.A. Sloane (1999). Sphere Packings, Lattices and Groups (3rd ed. ed.). New York: Springer-Verlag. ISBN 0-387-98585-9.